Formula Of Indefinite Integrals
(i) \dfrac{d}{dx} \dfrac{x^{n+1}}{n+1} = x^n , n \ne -1
(ii) \dfrac{d}{dx}(log | x | ) = \dfrac{1}{x}
\Rightarrow \int \dfrac{1}{x} d x = log | x | + C , when x \ne 0(iii) \dfrac{d}{dx} (e^x) = e^e
\Rightarrow \int e^x d x = e^x + C(iv) \dfrac{d}{dx} (\dfrac{1}{a} cosec^{-1} \dfrac{x}{a}) = \dfrac{-1}{x \sqrt{x^2 – a^2}}
\Rightarrow \int \dfrac{-dx}{x\sqrt{x^2 – a^2}} = \dfrac{1}{a} cosec^{-1} (\dfrac{x}{a}) + C(v) \dfrac{d}{dx} (\dfrac{1}{a}sec^{-1} \dfrac{x}{a}) = \dfrac{1}{x \sqrt{x^2 – a^2}}
\Rightarrow \int \dfrac{dx}{x \sqrt{x^2 – a^2}} = \dfrac{1}{a} sec^{-1} (\dfrac{x}{a}) + C(vi) \dfrac{d}{dx} (\dfrac{1}{a} cot^{-1} \dfrac{x}{a} ) = \dfrac{1}{a^2 + x^2}
\Rightarrow \int \dfrac{-1}{a^2 + b^2} d x = \dfrac{1}{a} cot^{-1} \dfrac{x}{a} + C(vii) \dfrac{d}{dx} (\dfrac{1}{a} tan^{-1} \dfrac{x}{a}) = \dfrac{1}{a^2 + b^2}
\Rightarrow \int \dfrac{dx}{a^2 + x^2 } = \dfrac{1}{a} tan^{-1} (\dfrac{x}{a}) + C(viii) \dfrac{d}{dx} (cos^{-1} \dfrac{x}{a}) = \dfrac{-1}{\sqrt{a^2 – x^2}}
\Rightarrow \int \dfrac{-1}{\sqrt{a^2 – x^2}} d x = cos^1 (\dfrac{x}{a}) + C(ix) \dfrac{d}{dx} (sin^{-1} \dfrac{x}{a}) = \dfrac{1}{\sqrt{a^2 – x^2}}
\Rightarrow \int \dfrac{dx}{\sqrt{a^2 – x^2}} = sin^1 (\dfrac{x}{a}) + C(x) \dfrac{d}{dx} (log | cosec x – cot x | ) = cosec x
\Rightarrow \int cosec x dx = log | cosec x – cot x | + C(xi) \frac{d}{d x} (-log|sin x | ) = cot x
\Rightarrow \int cot xdx = log | sin x | + C(xii) \frac{d}{dx} (- log | cos x |) = tan x
\Rightarrow \int tan xdx = – log | cos x | + C(xiii) \frac{d}{dx} ( log | sec x + tan x|) = sec x
\Rightarrow \int sec xdx = log | sec x + tan x| + C(xiv) \frac{d}{dx} ( log | cosec x – cot x|) = cosec x
\Rightarrow \int cosec xdx = log | cosec x – cot x| + C(xv) \frac{d}{dx} ( \sin^{-1} (\frac{x}{a})) = \frac{1}{\sqrt{a^2 – x^2}}
\Rightarrow \int \frac{dx}{\sqrt{a^2 – x^2}} = sin^{-1} (\frac{x}{a}) + C(xvi) \frac{d}{dx} ( \cos^{-1} (\frac{x}{a})) = \frac{-1}{\sqrt{a^2 – x^2}}
\Rightarrow \int \frac{-1}{\sqrt{a^2 – x^2}} dx = cos^{-1} (\frac{x}{a}) + C(xvii) \frac{d}{dx} (\frac{1}{a} \tan^{-1} (\frac{x}{a})) = \frac{1}{a^2 + x^2}
\Rightarrow \int \frac{dx}{a^2 + x^2} = \frac{1}{a} tan^{-1} (\frac{x}{a}) + C(xviii) \frac{d}{dx} (\frac{1}{a} \cot^{-1} (\frac{x}{a})) = \frac{-1}{a^2 + x^2}
\Rightarrow \int \frac{-1}{a^2 + x^2} dx = \frac{1}{a} \cot^{-1} (\frac{x}{a}) + C(xix) \frac{d}{dx} (\frac{1}{a} \sec^{-1} (\frac{x}{a})) = \frac{1}{x \sqrt{x^2 – a^2}}
\Rightarrow \int \frac{dx}{x \sqrt{x^2 – a^2}} = \frac{1}{a} \sec^{-1} (\frac{x}{a}) + C(xx)
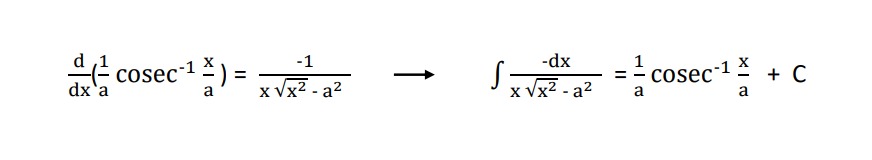
For video lecture visit here
for other study materials visit here