Electrostatic : Electric charge an electric field
Electro :- Related to electric charge
static:- at state of rest.
Electrostatic- The branch of physics in which we study about properties and phenomenon related to an electric charge, when it is at rest is known as electrostatic.
- Atom is electrically neutral because number of electrons is equal to the number of protons.
- when a body has deficiency or excess of electrons from normal due share, it is said to be charged.
- Conductors:– Those substance through which electric Charges Can flow easily are called conductors.
- Insulator:- Those substances through which electric Charges Can not flow are called insulator.
- Frictional electricity:- The electrostatic charges developed on insulating bodies when they are rubbed against each other is called frictional electricity.
- Methods of charging a conductor :
- By friction :- In this method the transfer of electrons between two materials when they rub against each other resulting in one materials becoming positively charged and other becoming negatively charged .
2. By conduction :- In this method , a charged body is brought in contact with the uncharged conductor .
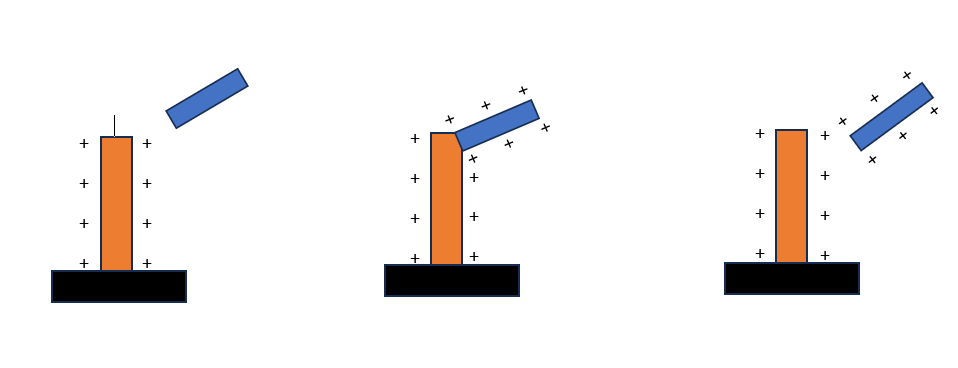
3. By Induction :- In this method a uncharged body is brought close to the charged conductor but does not touch .
- Charge :- Electric charge is the physical property of matter that causes it to experience a force when placed in an electromagnetic field
- It is a scalar quantity .
- It is represented by `Q` or `q` .
- Its S.I unit is coulomb (c) .
1C = 3 \times 10^9 stat coulomb (e.s.u)
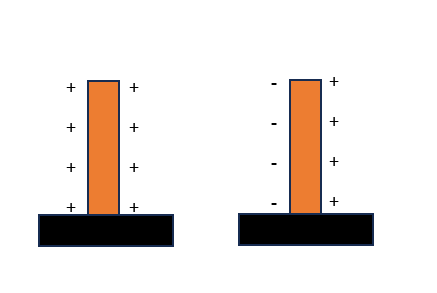
- properties of Electric charge.
- Quantization of electric charge :- It state that electric charge ση a body can only be exist in the integral multiple of electrons, It can’t be fractional.
Q = ne where , n = 1e, 2e,3e ………
Q = charge
N = no. of electrons
e = charge on an electrons.
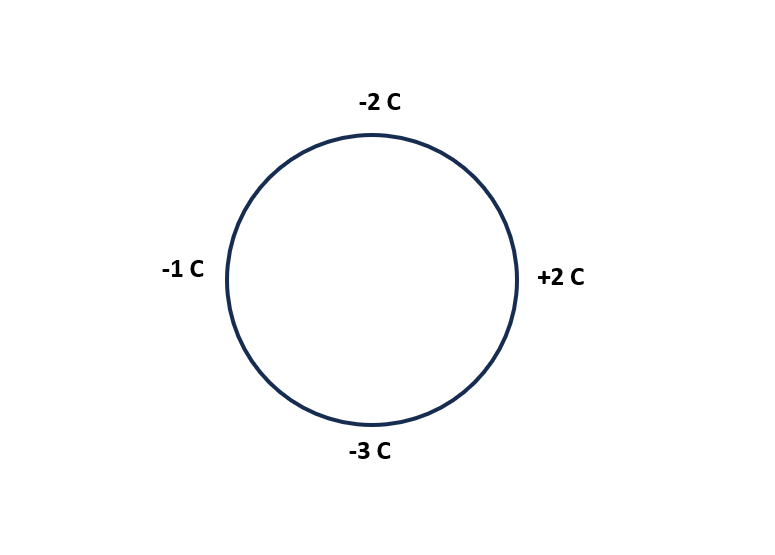
2. Additive property of electric charge :-
- Total charge on a body is equal to the algebraic Sum of all the individual electric charges present at its different parts.
Total charge = 7C – 2C – 3C
= 7C – 6C = 1C
3. Law of conservation of electric charge :
→ It state that electric charge Can neither be Created nor be destroyed, but it can only be transferred from one body to another body. total charge of a system is always conserved.
4. only two types of charge is possible either positive five or negative. third kind of charge is not possible.
→ Smaller units of charge
1 milli coulomb = 1mC = 10^{-3} C
1micro coulomb = 1 \mu C = 10^{-6} C
1nano coulomb = 1nC = 10^{-9} C
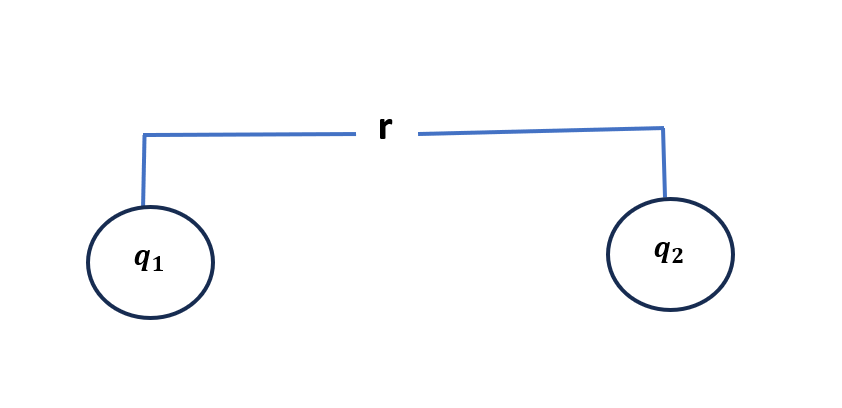
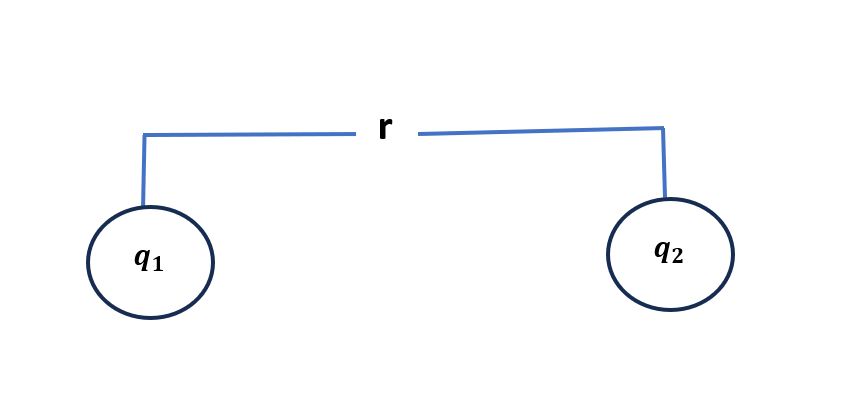
Coulomb’s law :- coulomb’s law fate that electrostatic force between Charges is directly proportional to the product of magnitude of charges and inversely proportional to square of distance between them.
F \propto q_1 q_2 \longrightarrow (i)
F \propto \frac{1}{r^2} \longrightarrow (ii)
F \propto \frac{q_1 q_2}{r^2}F = \frac{k q_1 q_2}{r^2} \longrightarrow where , k = proportionality constant.
or ,
F = \frac{1}{4 \pi \epsilon_o} \frac{ q_1 q_2}{r^2} \longrightarrow , where k = \frac{1}{4 \pi \epsilon_o} = 9 \times 10^9 Nm^2/C^2
Vector form of coulombs law
\bar F = \frac{1}{4 \pi \epsilon_o} \frac{ q_1 q_2}{r^2} \hat r_{12}or ,
\bar F = \frac{1}{4 \pi \epsilon_o} \frac{ q_1 q_2}{|\bar r_1 – \bar r_2|^3} (\bar r_1 – \bar r_2 )\epsilon_o = electrical permittivity of air / vacuum / free space
\epsilon_o = 8.85 \times 10^{-12} C^2 / Nm^2Limitations of coulomb’s Law
- It is only applicable for point charges at rest
- It holds good for very small distance up to about 10 m.
- this law can only be applied in the the case where the inverse square low is obeyed
- Electrical permittivity of a medium.
→ The surrounding medium of an electric charge has the property to transmit the electrical effect of an electric charge from one point to another without any physical or mechanical contact is Called electrical permittivity of medium.
or → The property of the medium which influence the electric force between the charges. as electrical permittivity is known as electrical permittivity.
→ It is represented by \epsilon
→ The permittivity of Known as air/vacuum/ free space permittivity is known as absolute electrical permittivity .
→ Electrical permittivity of force space fair/vacuum represented by E. (Epsilon naught)
→ \epsilon = 8.85 \times 10^{-12} C^2/NM^2 [M^{-1} L^{-3} T^4 A^2 ]
→ Dimensional formula of \epsilon is [M^{-1} L^{-3} T^4 A^2 ]
→ It is observed that the electric force between two point charges is maximum in free space.
→ A medium always reduces this electric force.
- Relative permittivity or dielectric constant.
→ F_{o} = \frac{1}{4 \pi \epsilon_{0}} \frac{q_{1} q_{2}}{r^2} ….. (i)
→ Force in other medium
F = \dfrac{1}{4 \pi \epsilon} \dfrac{q_{1} q_{2}}{r^2} ………(ii)
on dividing eq^n (i)/(ii) we get
\dfrac{F_{0}}{F} = \dfrac{\epsilon }{\epsilon_{0}} = \epsilon_{r} = K( \epsilon_{r} relative permittivity
K = dielectric constant )
\dfrac{\epsilon}{\epsilon_{0}} = \epsilon_{r}
\dfrac{\epsilon}{\epsilon_{0}} = K
\epsilon = \epsilon_{0}K
NOTE :- for metal \epsilon_{r} = \infty unit of \epsilon_{0} = C^2/NM^2 = Fm6{-1}
Thus, Relative permittivity is the ratio between electrical permittivity of the medium to the absolute permittivity of air or vacuum or free space
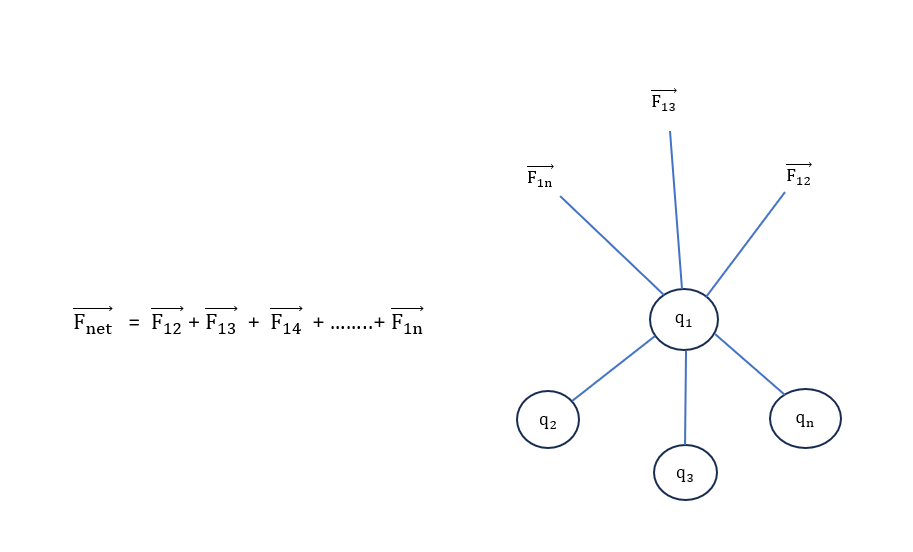
- Forces between multiple charges – (superposition principal)
→ It state that force on any charge due to a number of charges is vector sum of all forces on that Charges due to other charges taken one at a time The individual forces are unaffected due to presence of other charges.
- Continuous charge distribution
→ When an electric charge is distributed uniformly 0ver a body, then it is said to be continuous charge distribution.
\Rightarrow Types of continuous charge distribution.
(1). Linear charge distribution :- when electric charge distributed uniformly over length of a body it is called Linear charge distribution.
- It is the electric charge per unit length of a body.
- Linear charge density = \dfrac{electric charge}{length}
- t = \dfrac{q}{l}
→ Its S.I unit is C/M (coulomb/meter)
(2) . Surface charge distribution :- when electric charge is distributed uniformly over surface of a body then it is known as Surface charge distribution
- Surface charge density ( \sigma )
- It is the electric charge per unit area of a body
- It is represented by \sigma (sigma)
Surface charge density = \dfrac{charge}{area}
\sigma = \dfrac{q}{A}- Its S.I unit is c/m^2 (coulomb/meter^2)

(3). volume charge density :- when electric charge is distributed uniformly over volume of a body is known as volume charge distribution
- Volume charge density ( \rho )
- It is the electric charge per unit volume of a body
- It is represented by \rho (rho)
- Volume charge density = \dfrac{charge}{volume}
- \rho = \dfrac{q}{v}
- Its S.I unit is c/m^2 (coulomb/meter^2)
- Different between electrostatic force and gravitational force.
- ELECTROSTATIC FORCE
- It may be attractive or repulsive in nature
- It depends upon medium
- It is only applicable for point charge at rest.
- It is a strong force
- GRAVIATIONAL FORCE
- It is always attractive in nature
- It does not depend upon the medium
- It is applicable for masses both at rest and in motion
- It is weak force
→ Electrostatic or coulombic force is a conservative force
- Electric field: The space around an electric charge in which any other charge experiences some force is called electric field.

- Electric field intensity :- Electric field intensity is the force experienced by a unit positive test charge moving in the electric field
\Rightarrow from coulomb law .
F = \dfrac{K q_{1} q_{2} }{r^2}If q_{1} = q and q_{r} = q_{0} = 1
\therefore E = \dfrac{Kq}{r^2}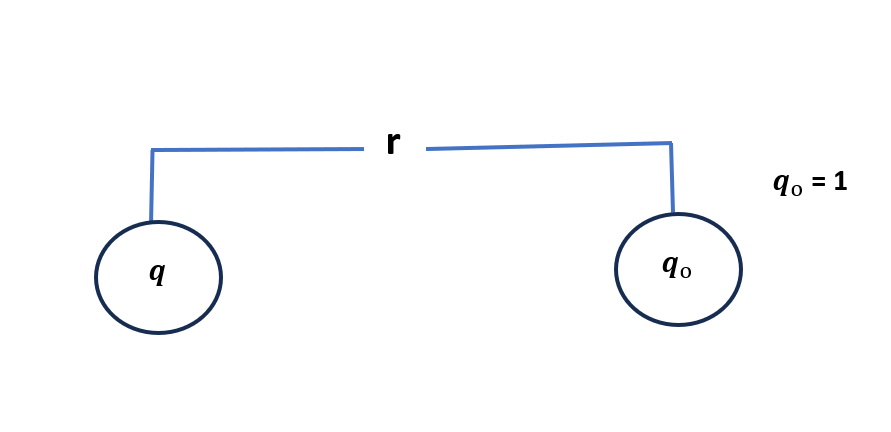
- Relation between electric field insity and force
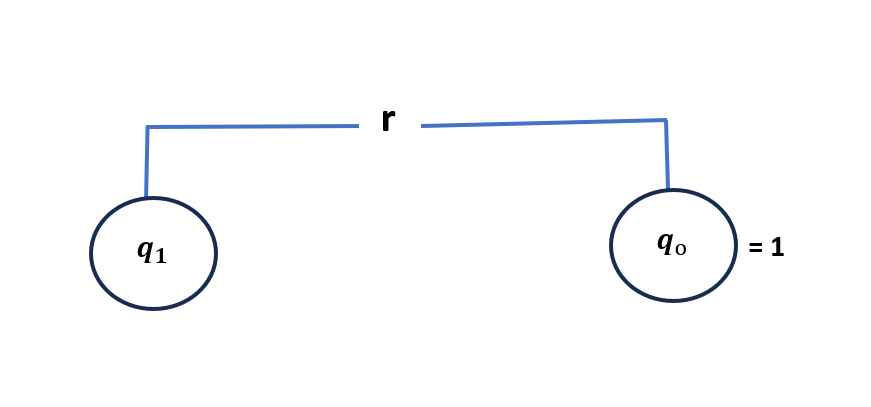
F = \dfrac{1}{4 \pi \epsilon_{0}} \dfrac{q q_{0}}{r^2} ….(i)
Electric field intensity (if q_{0} = 1 )
E = \dfrac{1}{4 \pi \epsilon_{0}} \dfrac{q_{0}}{r^2} …. (ii)On dividing equation (i)/(ii) we get ,
\dfrac{F}{E} = q_{0}\therefore E = \dfrac{F}{q_{0}} or F = qE
In vactor form
\overline{E} = \dfrac{\overline{F}}{q_{0}}
or, \overline{F} = q\overline{E}
→ Electric field intensity is a vector quantity.
→ Its S.I unit is N/C
→ its dimensional formula [M L T ^{-3} A^{-1} ]
→ It is always directed along the force experienced by unit positive test charge
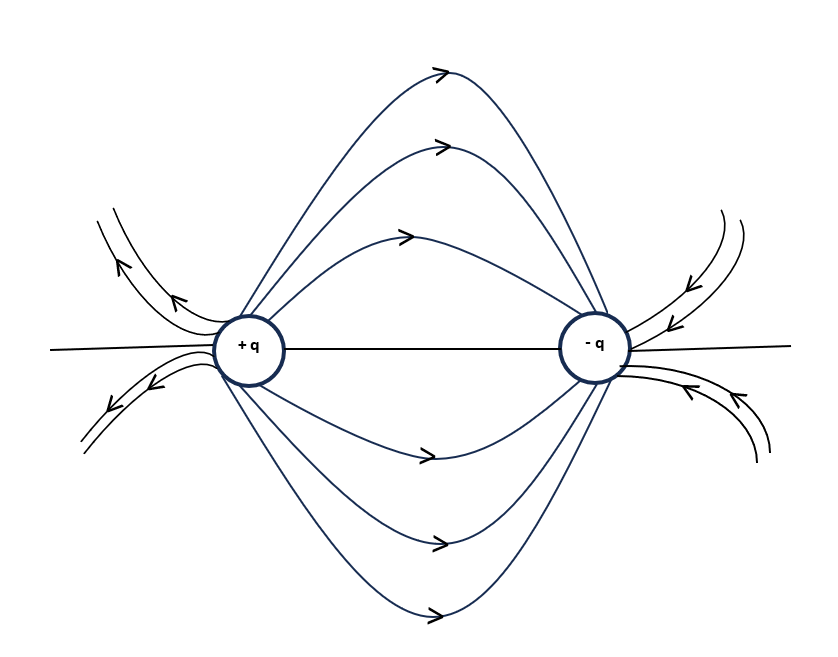
- Electric field lines or Electric five lines of force.
→ The path Followed by a unit positive test charge in an electric field. If it is free to move is Called electric field lines or electric lines of forces.
→ It may be straight or curved.
- properties of electric lines of force.
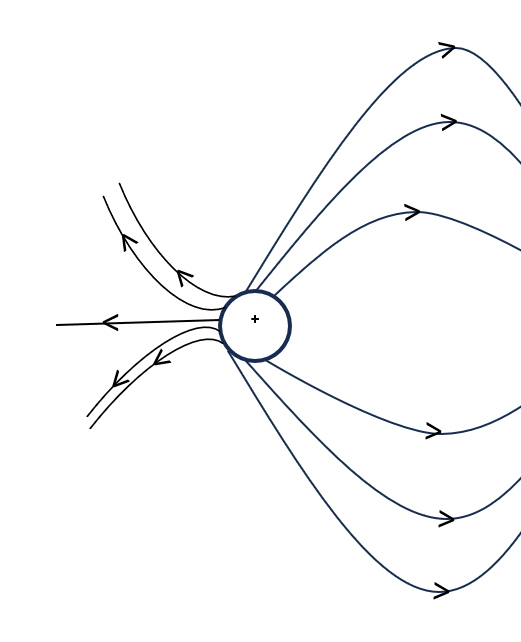
1 . It starts from a positive charge and end on a negative charge.
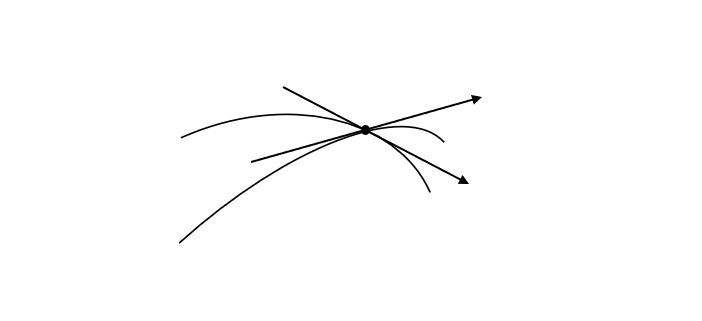
2. The tangent drawn at any point on electric field Lines gives the direction of electric charge field intensity at that point

3. Two electric field lines never intersect to each other.
4. It may be straight or Curved.
5. The density of Field lines indicates the strength of electric fields at given point.
NOTE :- Electric field Lines never intersect each other because at the point of intersection there will be two tangents. It means there are two direction of electric field at common point which is not possible.
- Field lines due to some charge configurations.
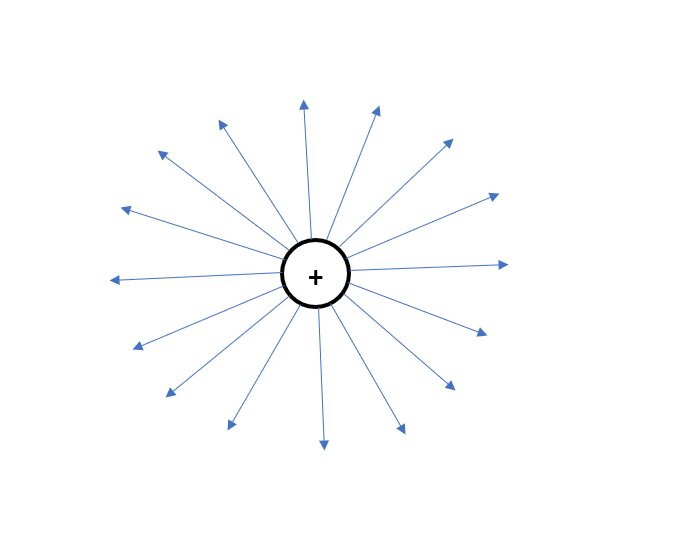
(a) Single position point charge.
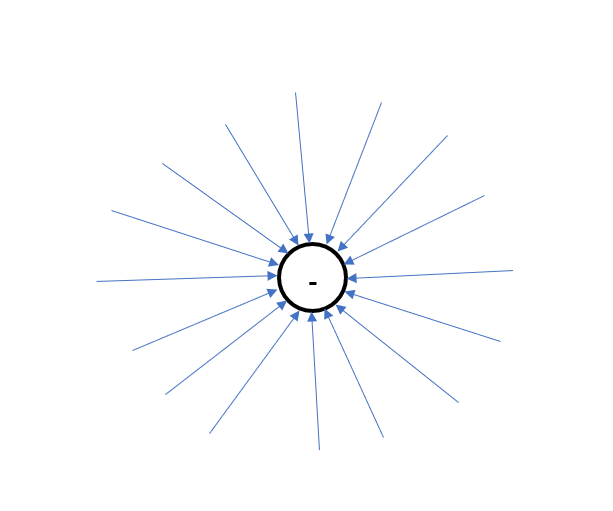
(b) Due to negative point charge
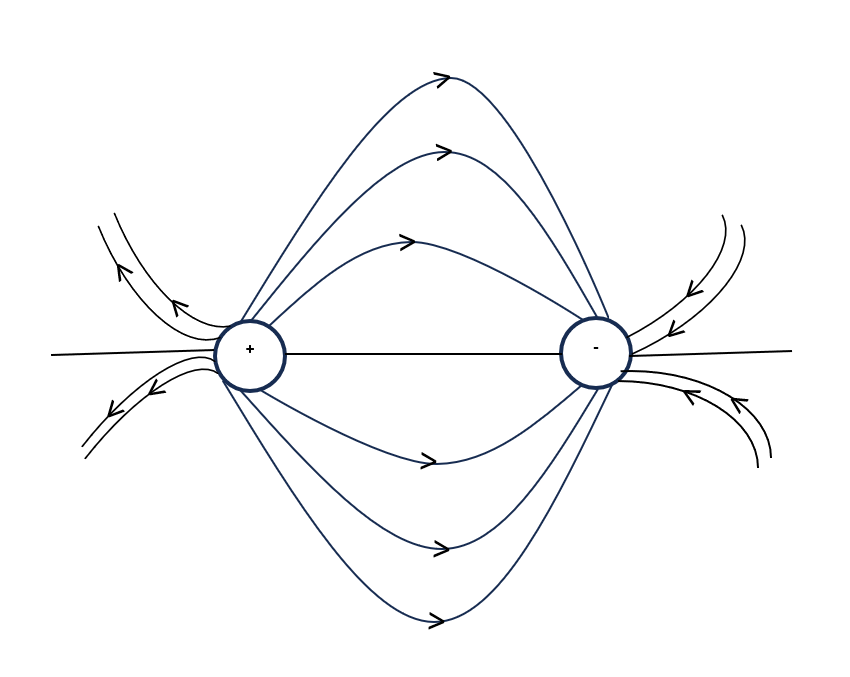
(c) Due to two equal and opposite charge
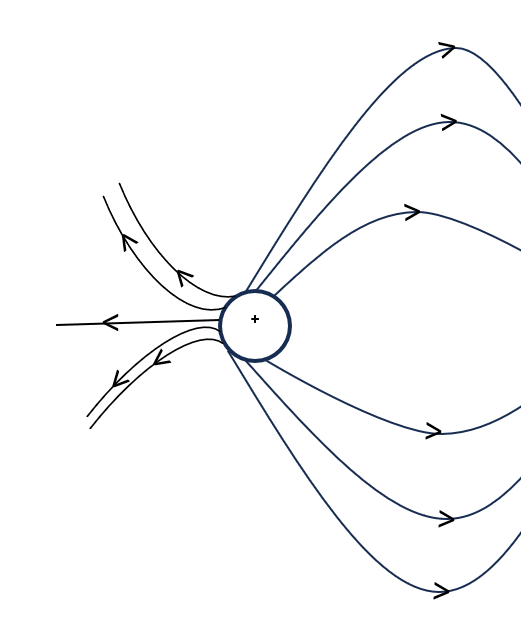
(d) Two equal positive point charge
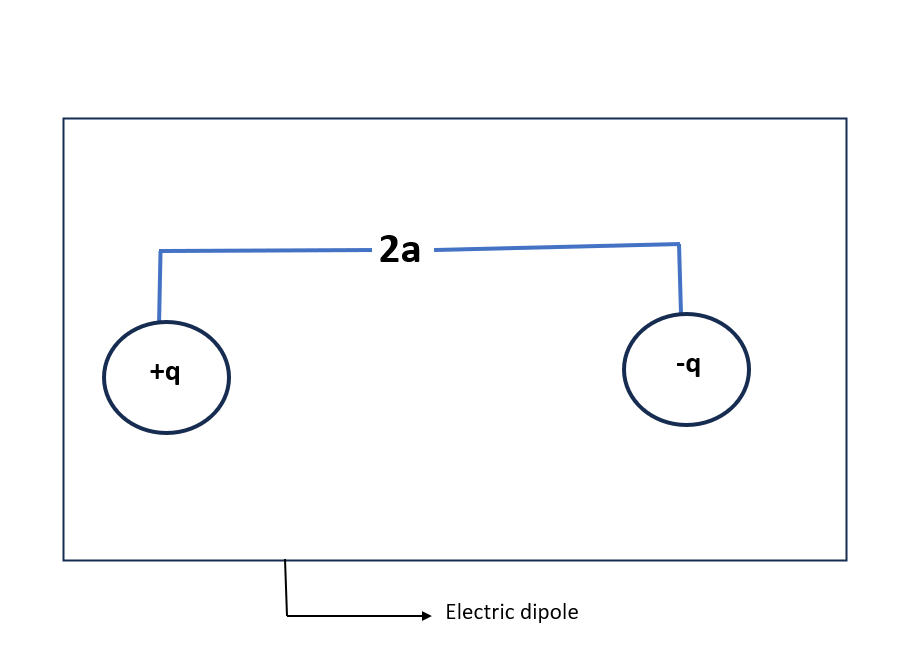
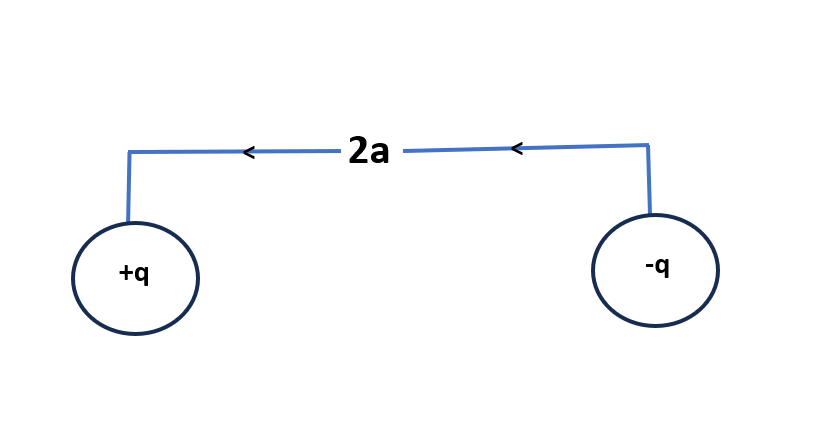
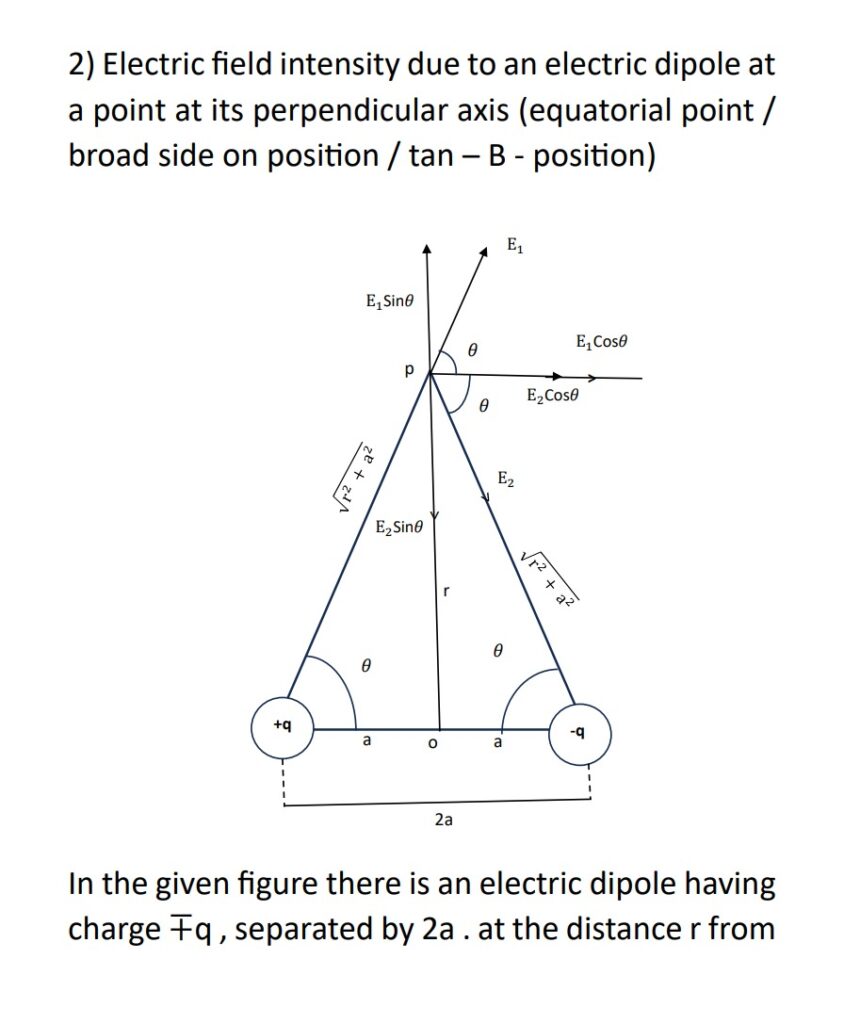
- Electric dipole : An electric dipole is a system of two equal and oppositive charges are seprated by Small distance of sepration.
- Electric dipole moment
→ Electric dipole Moment is numerically equal to the product of magnitude of either charge Length of the dipole
→ It is represented by `p`
p = q \times 2a→ It is a vector quantity, directed from negative Charge to positive charge of the dipole.
\overline{p} = q \times \overline{2a}→ Its S.I unit is C-M (coulomb – meter)
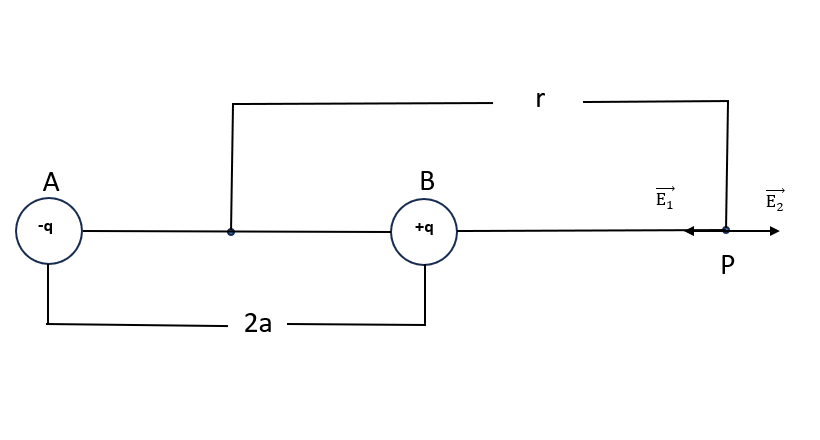
1. Electric field intensity on the axis of the dipole or. (axial poisstion/ end-on-position / tan-A-position)
→ In the given figure there is an electric dipole having charges q , seprated by distance `2a`. o’ is the centre of dipole. At the ‘r’ distance from the centre of the dipole a point ‘p’ is located on the axis of dipole where net electric field intensity to be calculated .
P = q \times 2a is the electric dipole moment.
→ Electric field intensity at point `p` due to `-q` charge
\overline{E_{1}} = \dfrac{kq}{(AP)^2} ……along \overline{PA}E_{1} = \dfrac{Kq}{(r+a)^2} ……(i)
Electric field intensity due to `+q` charge at point `p`
\overline{E_{2}} = \dfrac{kq}{(Bp)^2)} ….. along \overline{BP}E_{2} = \dfrac{Kq}{(r-a)^2} …..(ii)
Now net electric field intensity at `p`
\overline{E} = \overline{E_{2}} – \overline{E_{1}}E = \dfrac{kq}{(r-a)^2} …. from eq^n (i) &(ii)


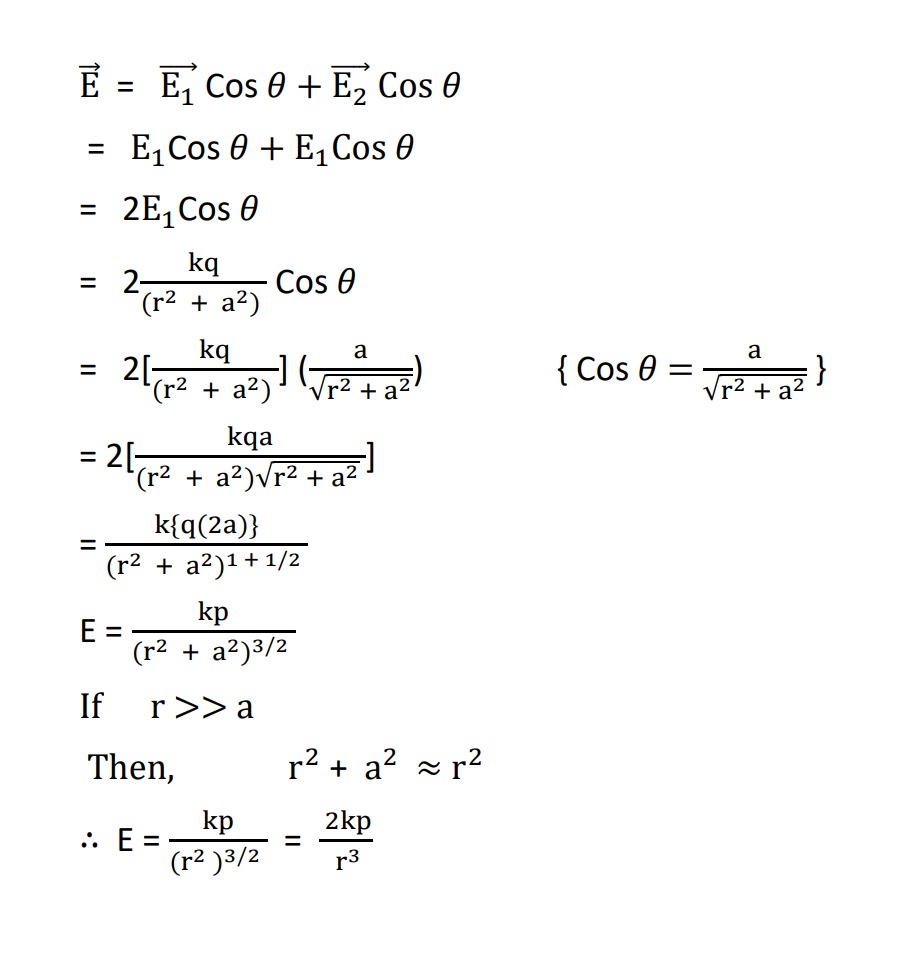
you may interested in the following :-
for video lecture you can visit here.