Class 10 chapter Trigonometry Question Bank

1. Q):- if sin A = $\frac{8}{17}$ , find other trigonometric ratios of $\angle A$ .

2. Q):- if cos A = $\frac{9}{41}$ , find other trigonometric ratios of $\angle A$ .

3. Q):- if tan A = $\sqrt{3}$ , find other trigonometric ratios of $\angle A$ .

4. Q):- if sin $\theta$ = $\frac{25}{7}$ , find other trigonometric ratios of $\theta$ .

5. Q):- if cos $\theta$ = $\frac{3}{5}$ , find the value of ( $\frac{5 cosec \theta – 4 tan \theta}{sec \theta + cot \theta}$ ) .

6. Q):- if sec $\theta = \frac{5}{4}$ , show that $\frac{(2 cos \theta – sin \theta)}{(cot \theta – tan \theta)} = \frac{12}{7}$ .

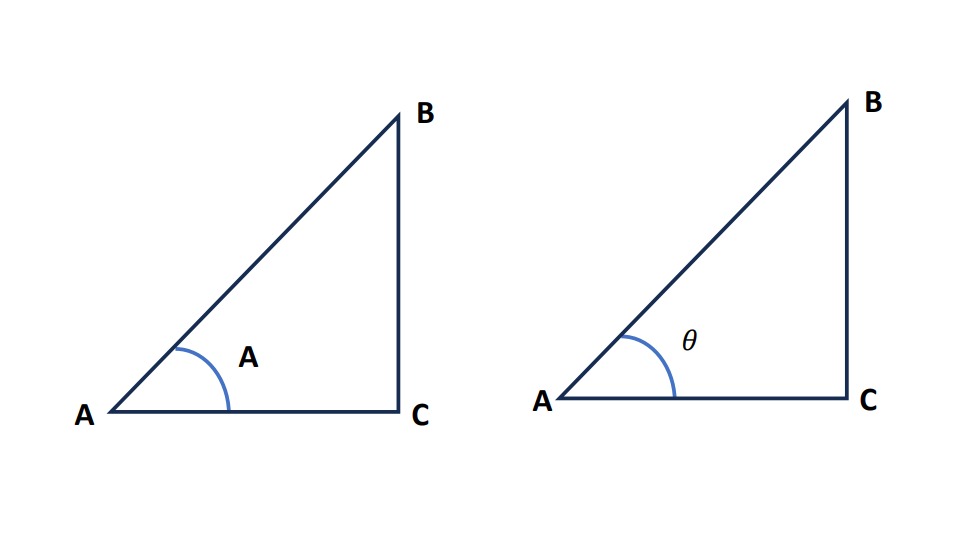
7. Q):- if $\triangle$ ABC it is given that $\angle B = {90}^\circ$ and AB : AC = 1 : $\sqrt{2}$ . find the value of ( $\frac{2 tan A}{1 + tan^2 A}$ ) .

8. Q):- if 3 tan $\theta$ = 4 , evaluate $\frac{3 sin \theta + 2 cos \theta }{3 sin \theta – 2 cos \theta}$ .

9. Q):- if 5cot $\theta$ = 3 , find the value of ( $\frac{5 sin \theta – 3 cos \theta}{4 sin \theta + 3 cos \theta}$ ) .

10. Q):- if $7 sin^2 \theta + 3 cos^2 \theta$ = 4 , show that tan $\theta = \frac{1}{\sqrt{3}}$ .

11. Q):- if cot $\theta = \frac{15}{8}$ , then evaluate $\frac{(2 + 2 sin \theta)(1 – sin \theta)}{(1 + cos \theta)(2 – 2 cos \theta)}$

12. Q):- in $\triangle$ ABC right – angled at B , AB = 5 cm and BC = 12 BC . find the values of sin A , sin C , sec A and sec C.

13. Q):- in a $\triangle ABC , \angle B = 90^{\circ}$ , AB = 5 cm and (BC + AC) = 25 cm . find the value of sin A , cos A , cosec C and sec C .

14. Q):- in a $\triangle ABC , \angle B = 90^{\circ}$ , AB = 7 cm and (AC – BC) = 1 cm . find the value of sin A , cos A , sin C , and cos C.

15. Q):- in a $\triangle ABC , \angle C = 90^{\circ}$ and tan A = $\frac{1}{\sqrt{3}}$ . find the value of

(i) sin A . cos B + cos A . sin B (ii) cos A . cos B – sin A . sin B

16.Q :- If $\angle A and \angle B$ are acute angle such that cos A = cos B then prove that $\angle A = \angle B.$

17. Q :- If sin $\theta = \dfrac{\sqrt{3}}{2},$ find the value of all T – ratio of $\theta$ .

18. Q :- If cos $\theta = \dfrac{\sqrt{7}}{25},$ find the values of all T-ratios of $\theta$ .

19. Q :- If tan $\theta = \dfrac{15}{8},$ find the values of all T-ratios of $\theta$ .

20. Q :- If cot $\theta$ = 2, find the values of all T-ratios of $\theta$ .

21. Q :- If cosec $\theta = \sqrt{10}$ , find the value of all T-ratio of $\theta$

22. Q :- If sin $\theta = \dfrac{a^2 – b^2}{a^2 + b^2},$ find the value of all T-ratios of $\theta$

23. Q :- If 15 cot A = 8 , find the values of sin A and sec A.

24. Q :- If sin A = $\dfrac{9}{41}$ , find the value of cos A and then tan A .

25. Q :- If cos $\theta = 0.6$ , show that (5 sin $\theta$ – 3 tan $\theta$ ).

26. Q :- If cosec $\theta$ = 2, show that $cot \theta + (\dfrac{sin \theta}{1+cos \theta}$ ) = 2.

27. Q :- If tan $\theta = \dfrac{1}{\sqrt7}$ , show that $\dfrac{cosec^2 \theta – sec^2}{cosec^2 \theta + sec^2 \theta} = \dfrac{3}{4}$

28. Q :- If tan $\theta = \dfrac{20}{21}$ , show that $\dfrac{1 – sin\theta + cos\theta}{1 + sin\theta + cos\theta} = \dfrac{12}{7}.$

29. Q :- If cot $\theta = \dfrac{3}{4},$ show that $\sqrt\dfrac{sec \theta – cosec \theta}{sec \theta + cosec \theta} = \dfrac{1}{\sqrt7}$ .

30. Q :- If sin $\theta = \dfrac{3}{4}$ , show that $\sqrt\dfrac{cosec^2 \theta – cot^2 \theta}{sec^2 \theta – 1} = \dfrac{\sqrt7}{3}.$

31. Q :- If sin $\theta = \dfrac{a}{b},$ show that (sec $\theta + tan\theta ) = \sqrt\dfrac{b + a}{b – a}.$

32. Q :- If cos $\theta = \dfrac{3}{5}$ , show that $\dfrac{sin \theta – cot \theta}{2tan\theta} = \dfrac{3}{160}.$

33. Q :- If tan $\theta = \dfrac{4}{3} ,$ show that $(sin\theta + cos \theta) = \dfrac{7}{5}$ .

34. Q :- If tan $\theta = \dfrac{a}{b},$ show that $(\dfrac{a sin\theta – b cos \theta}{ a sin\theta + b cos \theta}) = (\dfrac{a^2 – b^2}{a^2 + b^2})$ .

35. Q :- If 3 tan $\theta$ = 4 , show that $(\dfrac{4 cos \theta – sin \theta}{2 cos \theta + sin \theta }) = \dfrac{4}{5}.$

36. Q :- If 3cot $\theta$ = 2 show that $(\dfrac{4sin \theta – 3cos \theta}{2sin \theta + 6cos \theta }) = \dfrac{1}{3}$ .

37. Q :- If 3 cot $\theta = 4$ , show that $\dfrac{3 – 4tan^2 \theta}{4tan^2 \theta – 3 } = (cos^2 \theta – sin^2 \theta )$ .

38. Q :- If sec $\theta = \dfrac{17}{8},$ verify that ( $\dfrac{3 – 4 sin^2 \theta}{4cos^2\theta – 3 } = (\dfrac{3 – tan^2 \theta}{1 – 3tan^2 \theta })$ .

39. Q :- In a $\Delta ABC, \angle B = 90 \degree$ AB = 24 cm and BC = 7 cm.

Find (i) sin A (ii) cos A (iii) sin C (iv) cos C.

40. Q :- In a $\Delta ABC, \angle C = 90 \degree , \angle ABC = \theta ,$ , BC = 21 units and AB = 29 units.

show that $(cos^2 \theta – sin^2 \theta ) = \dfrac{41}{841}.$

for other chapter question bank visit here

model paper class 10

and for video lecture on trigonometry visit here.