Triangle class 10

Congruent figures : Two geometric figures which have the same shape and size are known as congruent figures.
Similar figures : geometric figures which have same shape but different sizes are known as similar figures.
Two congruent figures are always similar but two similar figures need not be congruent.
SIMILAR POLYGONS : Two polygons having the same number of sides are said to be similar, if
(i) their corresponding angles are equal, and
(ii) the lengths of their corresponding sides are proportional.
if two polygons ABCDE and PQRST are similar, we write, ABCDE ~ PQRST , where the symbol ‘~’ stands for similar to’
The constant ratio between the corresponding sides of two similar figures is known as the scale factor, or the representative fraction. Since triangles are also polygons, so the same set of condition apply for the similarity of triangles.
EQUIANGULAR TRIANGLES : Two triangles are said to be equiangular if their corresponding angles are equal.
SIMILAR TRISNGLES : Two triangle are said to be similar to each other if,
(i) their corresponding angles are equal, and
(ii) their corresponding sides are proportional.
Basic proportionality theorem (b.p.t) or Thales theorem

*)Thales' Theorem
Here Thales’ theorem is describe by two method and named as method – 1 and method – 2. and for video of these theory click on the respective method
please read the below pdf in which Thales’ theorem has been describe
Method -1st
Method -2nd
*)converse of Thales' Theorem video lecture :-
Converse of thales' theorem
we have already learned the two mothed of Thales’ theorem in detailed way. each and every point have been discussed in that two method if you have not seen or gone through that lecture then please visit here for video lecture method -1 and method -2 and click here for notes
following is the brief of Converse of thales’ theorem

CRITERIA FOR SIMILARITY OF TWO TRIANGLES
(AAA-SIMILARITY) : If in two triangle, the corresponding angle are equal, then their corresponding sides are proportional and hence the triangle are similar.
Given :- \Delta ABC and \Delta DPQ, WE have
To prove : \Delta ABC ~ \Delta
Construction : Cut DP = AB and DQ = AC . join PQ
AB = DP [by construction]
AC = DQ [by construction]
\angle A = \angle D [given]
\therefore \Delta ABC \cong \Delta DPQ [by SAS-congruence]
\angle B = \angle p
\angle E = \angle p [ \because \angle B = \angle E (given)]
PQ || EF [ \because corresponding \angle s are equal ]
\dfrac{DP}{DE} = \dfrac{DQ}{DF}
\dfrac{AB}{DE} = \dfrac{CA}{FD} [ \because DP = AB and DQ = AC ]
Similarly , \dfrac{AB}{DE} = \dfrac{BC}{EF} .
\therefore \dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{CA}{FD} .
Thus, \angle A = \angle D , \angle B = \angle E , \angle C = \angle F and \dfrac{ AB}{DE} = \dfrac{BC}{EF} = \dfrac{CA}{FD} .
Hence, \Delta ABC \sim \Delta DEF.
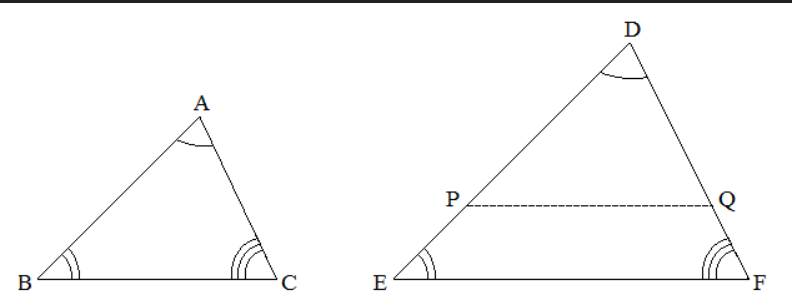
( AA-SIMILARITY ) : If two angles of one triangle are respectively equal to two angles of another triangle then the two triangles are similar.
Proof : In \Delta ABC = \Delta DEF , let \angle A = \Delta D and \angle B = \angle E .
Then, 3rd \angle C = 3rd \angle F .
AA-similarity is the same as AAA-similarity.
SSS-SIMILARITY : If the corresponding sides of two triangles are proportional then their corresponding angles are equal, and hence the two tringles are similar.
Given :- \Delta ABC and \Delta DEF in which \dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF} .
Prove :- \Delta ABC \sim \Delta DEF .
Construction :- Let us take \Delta ABC and \Delta DEF such that
\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF} (<1).
Cut DP = AB and DQ = AC. Join PQ.
Proof :- \dfrac{AB}{DE} = \dfrac{AC}{DF} \Rightarrow \dfrac{DP}{DE} = \dfrac{DQ}{DF} [ \because AB = DP and AC =DQ]
So, by the converse of thales’ theorem , PQ || EF.
\therefore \angle P = \angle E [corresponding \angle s ]
\angle Q = \angle F [corresponding \angle s ]
\therefore \Delta DPQ \sim \Delta DEF [by AA-similarity]
\Rightarrow \dfrac{DP}{DE} = \dfrac{PQ}{EF}
\Rightarrow \dfrac{AB}{DE} = \dfrac{PQ}{EF}. …..(i) [ \because DP = AB ]
But \dfrac{AB}{DE} = \dfrac{BC}{EF}. …..(ii) [given]
\because \dfrac{PQ}{EF} = \dfrac{BC}{EF} [from(i) and (ii) ]
\Rightarrow BC = PQ .
Thus, AB = DP, AC = DQ and BC = PQ.
\therefore \Delta ABC \cong \Delta DPQ [by SSS – similarity ]
\therefore \angle A = \angle D , \angle B = \angle P = \angle and \angle C = \angle Q =\angle F
\Rightarrow \angle A = \angle D , \angle B = \angle E and \angle C = \angle F .
Thus, the given triangle are equiangular and hence similar.
Given :- \Delta ABC and \Delta DEF in which \angle A = \angle D and \dfrac{AB}{DE} = \dfrac{AC}{DF}
To prove :- \Delta ABC \sim \Delta DEF.
CONSTRUCTION:- Let us take \Delta ABC and \Delta DEF such that
\dfrac{AB}{DE} = \dfrac{AC}{DF} (<1) and \angle A = \angle D.
Cut DP = AB and DQ =AC. Join PQ.
Proof :- In \Delta ABC and \Delta DPQ , we have
AB = DP [ by construction ]
\angle A = \angle D [given]
AC = DQ [by construction]
\therefore \Delta ABC \cong \Delta DPQ [by SAS – congruence]
\therefore \angle A = \angle D , \angle B = \angle P and \angle C = \angle Q.
Now, \dfrac{AB}{DE} = \dfrac{AC}{DF} (given)
\Rightarrow \dfrac{DP}{DE} = \dfrac{DQ}{DF} [\because AB = DP and AC = DQ ]
\Rightarrow PQ || EF [ By the converse of thales' theoram ]
\Rightarrow \angle P = \angle E and \angle Q = \angle F [ corresponding \angle s ]
\therefore \angle A = \angle D , \angle B = \angle P = \angle E and \angle C = \angle Q = \angle F.
Thus, \angle A = \angle D , \angle B = \angle E , \ angle C = \angle F.
So, the given triangle are equiangular and hence similar.
Given :- A \Delta ABC in which \angle BAC = 90\degree and AD \perp BC
To prove (i) \Delta DBA \sim \Delta ABC
(ii) \Delta DAC \sim \Delta ABC
(iii) \Delta DBA \sim \Delta DAC
Proof :- (i) In \Delta DBA and \Delta ABC, we have
\angle BDA = \angle BAC = 90 \degree
\angle DBA = \angle ABC (common)
\therefore \Delta DBA \sim \Delta ABC [by AA- similarity ]
(ii) In \Delta DAC and \Delta ABC , we have
\angle CDA = \angle CAB = 90 \degree
\angle DCA = \angle ACB (common)
\therefore \Delta DAC \sim \Delta ABC [ By AA- similarity ].
(iii) In \Delta DBA and \Delta DAC, we have
\angle ADB = \angle CDA = 90 \degree [/latex]
\therefore \angle B + \angle BAD = 90\degree …(1)
\angle C + \angle CAD = 90 \degree …(2)
\angle BAD + \angle CAD = 90 \degree …(3)
form (1) ,(2) and (3)
\Rightarrow \angle B = \angle CAD and \ C and \angle BAD .
Thus, in \Delta DBA and \ DAC we have :
\angle ADB = \angle CDA [each equal to 90 \degree ]
\angle B = \angle CAD
\angle BAD = \angle C
\therefore \Delta DBA \sim \Delta DAC [ by AAA – similarity ]
Theorem : – If two triangle are equiangular , prove that the ratio of their corresponding sides is the same as the ratio of the corresponding altitudes .
\Delta ABC and \Delta DEF in which \angle A = \angle D , \angle B = \angle E and \angle C = \angle F and AF \perp BC and DM \perp EF.TO PROVE : \dfrac{BC}{EF} = \dfrac{AL}{DM}
PROOF : Since \Delta ABC and \Delta DEF are equiangular , \Delta ABC \sim \Delta DEF.
\therefore \dfrac{AB}{DE} = \dfrac{BC}{EF}
In \Delta ALB and \Delta DME , we have
\angle ALB = \angle DME = 90\degree and \angle B = \angle E (given) .
\therefore \Delta ALB \sim \Delta DME [ by AA – SIMILARITY ]
\therefore \dfrac{AB}{DE} = \dfrac{AL}{DM}.
form (i) and (ii) , we get \dfrac{BC}{EF} = \dfrac{AL}{DM}
Theorem : If two triangle are equiangular , prove that the ratio of their corresponding sides is the same as the ratio of the corresponding medians.
GIVEN : \Delta ABC and \Delta DEF in which \angle A = \angle D , \angle B = \angle E and \angle C = \angle F and AL and DM are the medians
TO PROVE : \dfrac{BC}{EF} = \dfrac{AL}{DM}
PROOF : Since \Delta ABC and \Delta DEF are equiangular , we have \Delta ABC \sim \Delta DEF
\therefore \dfrac{AB}{DE} = \dfrac{BC}{EF}. …(i)
But, \dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{2BL}{2EM} = \dfrac{BL}{EM}.
Now , in \Delta ABL and \Delta DEM , we have \dfrac{AB}{DE} = \dfrac{BL}{EM} and \angle B = \angle E (given).
\therefore \Delta ABL \sim \Delta DEM [by SAS – similarity ]\Rightarrow \dfrac{AB}{DE} = \dfrac{AL}{DM} . …..(ii)
From (i) and (ii) , we get \dfrac{BC}{EF} = \dfrac{AL}{DM}.
Theorem : If two triangle are equiangular , show that the ratio of the corresponding sides is the same as the ratio of the corresponding angle – bisector segments.
Given : \Delta ABC and \Delta DEF in which \angle A = \angle D , \angle B = \angle E and \angle C = \angle F , and AX and DY are the bisectors of \angle A and \angle D respectively .
TO Prove : \dfrac{BC}{EF} = \dfrac{AX}{DY}
Proof : Since \Delta ABC and \Delta DEF are equiangular, we have \Delta ABC \sim \Delta DEF .
\therefore \dfrac{AB}{DE} = \dfrac{BC}{EF} ….. (i)Now, \angle A = \angle D \Rightarrow \dfrac{1}{2} \angle A = \dfrac{1}{2} \angle D \Rightarrow \angle BAX = \angle EDY .
Thus, in \Delta ABX and \Delta DEY , we have
\angle BAX = \angle EDY (proved) \angle B = \angle E (given) \therefore \Delta ABX \sim \Delta DEY [ by AA – similarity ] \Rightarrow \dfrac{AB}{DE} = \dfrac{AX}{DY} . ….(ii)From (i) and (ii) , we get \dfrac{BC}{EF} = \dfrac{AX}{DY}.
THEOREM : The ratio of the areas of two similar triangle is equal to the ratio of the squares of their corresponding sides.
GIVEN : \Delta ABC \sim \Delta DEF .
TO PROVE : \dfrac{ar \Delta ABC}{ar \Delta DEF} = \dfrac{AB^2}{DE^2} = \dfrac{AC^2}{DF^2} = \dfrac{BC^2}{EF^2}
CONSTRUCTION : Draw AL \perp BC and DM \perp EF . .
PROOF : Since \Delta ABC \sim \Delta DEF , it follows that they are equiangular and their side are proportional .
\therefore \angle A = \angle D , \angle B = \angle E , \angle C = \angle F and \dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}. …..(i)Now, ar (\Delta ABC ) = (\dfrac{1}{2} \times BC \times AL )
and , ar (\Delta DEF ) = (\dfrac{1}{2} \times EF \times DM ).
\therefore ( \dfrac{ar \Delta ABC}{ar \Delta DEF}) = \dfrac{ \dfrac{1}{2} \times BC \times AL}{\dfrac{1}{2} \times EF \times DM } = \dfrac{BC}{EF} \times \dfrac{AL}{DM}. ….(ii)Also, \dfrac{AL}{DM} = \dfrac{BC}{EF} …(iii) [\because in similar triangles, the ratio of the corres . sides is the same as the ratio of corresponding altitudes ]
Using (iii) in (ii) , we get
\dfrac{ar \Delta ABC}{ar \Delta DEF} = (\dfrac{BC}{EF} \times \dfrac{BC}{EF}) = \dfrac{BC^2}{EF^2}
Similarly, \dfrac{ar \Delta ABC}{ar \Delta DEF} = \dfrac{AB^2}{DE^2} and \dfrac{ar \Delta ABC}{ar \Delta DEF} = \dfrac{AC^2}{DF^2}
Hence, \dfrac{ar \Delta ABC}{ar \Delta DEF} = \dfrac{AB^2}{DE^2} = \dfrac{AC^2}{DF^2} = \dfrac{BC^2}{EF^2}